[문제링크]
https://www.acmicpc.net/problem/14501
문제 설명
상담원으로 일하고 있는 백준이는 퇴사를 하려고 한다.
오늘부터 N+1일째 되는 날 퇴사를 하기 위해서 남은 N일동안 최대한 많은 상담을 하려고 한다.
하루에 하나씩 서로 다른 사람의 상담이 잡혀있고, 각각의 상담은 상담을 완료하는 데 걸리는 시간 T_i, 상담을 했을 때 받을 수 있는 금액 P_i로 이루어져 있다.
하나의 상담을 하는데 필요한 기간이 1일보다 클 수 있기 때문에 모든 상담을 수행할 수 없다.
예를 들어 N=7인 경우 상담 일정표가 다음과 같을 때,
1일의 상담을 수행하면 2일, 3일의 상담은 수행할 수 없다.
N+1일 이후부터는 회사에 없기 때문에 6일, 7일의 상담은 수행할 수 없다.

퇴사 전 할 수 있는 상담의 최대 이익은 1일, 4일, 5일의 상담을 하는 것이고, 이 때 이익은 10+20+15=45이다.
상담을 적절히 했을 때, 백준이가 얻을 수 있는 최대 수익을 구하는 프로그램을 작성하시오.
입력조건
- 첫째 줄에 N
- 둘째 줄부터 N개의 줄에 T와 P를 공백으로 구분지어서 입력
출력조건
- 백준이가 얻을 수 있는 최대 이익
입출력 예시
| 입력예시 | 출력예시 |
| 7 3 10 5 20 1 10 1 20 2 15 4 40 2 200 |
45 |
| 10 1 1 1 2 1 3 1 4 1 5 1 6 1 7 1 8 1 9 1 10 |
55 |
문제 풀이
백트래킹과 다이나믹프로그래밍 2가지 방법으로 문제를 풀어보았다.
이 예시를 가지고 문제를 이해하며 풀어보았다.
(배열인덱스때문에 0부터 시작했지만 실제로는 1일부터를 나타내고, 현재날짜를 의미한다.)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| T | 3 | 5 | 1 | 1 | 2 | 4 | 2 |
| P | 10 | 20 | 10 | 20 | 15 | 40 | 200 |
그 전에 특정 상담이 가능한지 아닌지 판단하는 과정을 알아본다.
T[1]=5의 경우, 5일동안 상담을 하고나면 i=6으로 간다.
T[3]=1의 경우, 1일동안 상담을 하고나면 i=4로 간다.
T[5]=4의 경우, 퇴사일을 넘기기 때문에 상담 자체가 불가능하다.
T[6]=2의 경우, 퇴사일을 넘기기 때문에 상담 자체가 불가능하다.
현재날짜를 나타내는 인덱스(i)에 현재날짜의 상담을 진행하는데 걸리는 시간(T[i])을 더한 값이 전체일수(n)보다 작거나 같으면 해당 상담을 할 수 있다.
즉, i + T[i] <= n 이 성립하면 상담이 가능하다.
1️⃣ 백트래킹 풀이
재귀호출을 활용해서 백트래킹으로 문제를 풀 수 있다.
먼저 가능한 경우를 트리구조로 그려보면 다음과 같다.

- index=현재날짜, points=현재까지 얻은 이익
- 상담을 진행할 경우와 진행하지 않을 경우로 나눠서 생각한다.
- 상담을 진행할 경우 : 상담이 가능한지 확인 후 가능하다면 index+T[index](현재상담하는데 걸리는 기간),
points+P[index](현재상담으로 얻는 이익) 해서 재귀호출 - 상담을 진행하지 않을 경우 : index+1 해서 재귀호출
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static int[] T;
public static int[] P;
public static int n = 0, ans = 0;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
n = Integer.parseInt(br.readLine()); //퇴사 전까지 남은 일수
T = new int[n];
P = new int[n];
for (int i = 0; i < n; i++) {
st = new StringTokenizer(br.readLine());
T[i] = Integer.parseInt(st.nextToken());
P[i] = Integer.parseInt(st.nextToken());
}
dfs(0, 0);
System.out.println(ans);
}
public static void dfs(int index, int points) { //index:현재날짜, point: 현재까지 얻은 수익
//종료조건
if (index >= n) {
ans = Math.max(ans, points); //수익이 가장 큰 것으로 변경
return;
}
//상담을 진행할 경우
if (index + T[index] <= n) {
dfs(index + T[index], points + P[index]);
}
//상담을 진행하지 않는 경우
dfs(index + 1, points);
}
}
2️⃣ 다이나믹 프로그래밍 풀이
뒤에서부터 역방향으로 접근해서 최대 이익을 구해서 dp테이블을 완성한다.
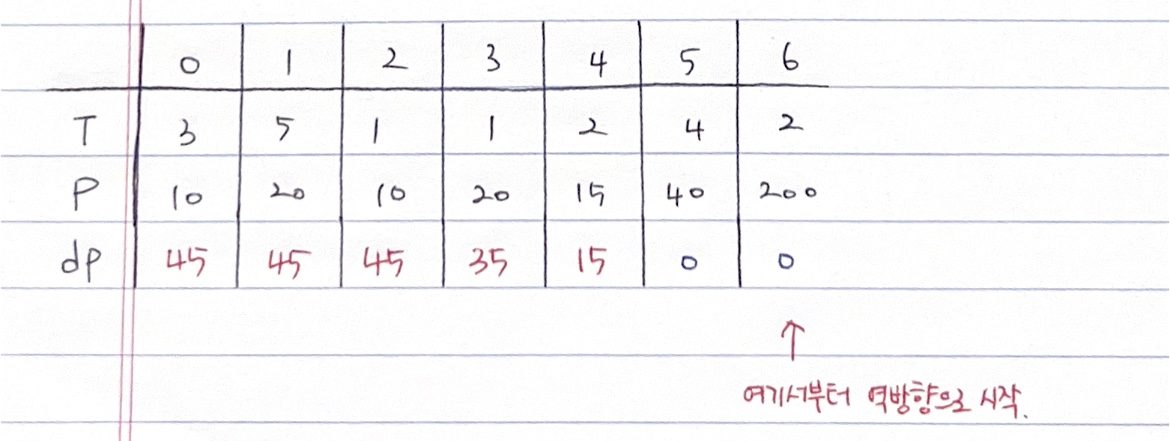
dp[i] : i번째 상담 진행여부를 결정했을 때의 최대 이익
- dp[6] = 0 → 6 + 2(T[6]) >= 7이므로 상담 자체가 불가능하다.
- dp[5] = 0 → 5 + 4(T[5]) >= 7이므로 상담 자체가 불가능하다.
- dp[4] = 15
- 4 +2(T[4]) <= 7이기 때문에 상담을 진행할 수 있다.
- 상담을 진행할 경우 : 현재부터 2일 후의 이익 최댓값(dp[6])+현재 상담의 이익(P[4]) = 15
- 상담을 진행하지 않을 경우 : 다음 날의 이익 최댓값(dp[5]) = 0
- dp[3] = 35
- 3 +1(T[3]) <= 7이기 때문에 상담을 진행할 수 있다.
- 상담을 진행할 경우 : 현재부터 1일 후의 이익 최댓값(dp[4]) + 현재 상담의 이익(P[3]) = 35
- 상담을 진행하지 않을 경우 : 다음 날의 이익 최댓값(dp[4]) = 15
- dp[2] = 45
- 2 +1(T[2]) <= 7이기 때문에 상담을 진행할 수 있다.
- 상담을 진행할 경우 : 현재부터 1일 후의 이익 최댓값(dp[3]) + 현재 상담의 이익(P[2]) = 45
- 상담을 진행하지 않을 경우 : 다음 날의 이익 최댓값(dp[3]) = 35
- dp[1] = 45
- 1 +5(T[1]) <= 7이기 때문에 상담을 진행할 수 있다.
- 상담을 진행할 경우 : 현재부터 5일 후의 이익 최댓값(dp[6]) + 현재 상담의 이익(P[2]) = 20
- 상담을 진행하지 않을 경우 : 다음 날의 이익 최댓값(dp[2]) = 45
- dp[0] = 45
- 0 +3(T[0]) <= 7이기 때문에 상담을 진행할 수 있다.
- 상담을 진행할 경우 : 현재부터 3일 후의 이익 최댓값(dp[3]) + 현재 상담의 이익(P[0]) = 45
- 상담을 진행하지 않을 경우 : 다음 날의 이익 최댓값(dp[1]) = 45
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static int[] T;
static int[] P;
static int n;
static int[] dp = new int[16];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
n = Integer.parseInt(br.readLine()); //퇴사 전까지 남은 일수
T = new int[n];
P = new int[n];
for (int i = 0; i < n; i++) {
st = new StringTokenizer(br.readLine());
T[i] = Integer.parseInt(st.nextToken());
P[i] = Integer.parseInt(st.nextToken());
}
for (int i = n - 1; i >= 0; i--) {
if (i + T[i] <= n) { //상담 가능한 경우
//상담 가능한 경우라도 상담을 할수도, 하지 않을 수도 있다.
//1. i번째 날의 상담을 할 경우: P[i] + dp[i + T[i]]
//2. i번째 날의 상맏을 하지 않을 경우 : dp[i + 1]
dp[i] = Math.max(P[i] + dp[i + T[i]], dp[i + 1]);
}
else { //상담 불가능한 경우
dp[i] = dp[i + 1];
}
}
System.out.println(dp[0]);
}
}[참고]
이것이 취업을 위한 코딩 테스트다 with 파이썬 by 나동빈
'PS > 이코테' 카테고리의 다른 글
| [이코테][Java] 문자열 압축 (0) | 2025.06.01 |
|---|---|
| [백준][Java] 14502번 : 연구소 (0) | 2025.06.01 |
| [이코테][Java] 연산자 끼워넣기 (0) | 2025.05.12 |
| [이코테][Java] 병사 배치하기 (0) | 2025.04.29 |
| [이코테][Java] 편집거리 (0) | 2025.04.27 |