다이나믹 프로그래밍이란?
큰 문제를 작은 문제로 쪼개고, 같은 문제라면 한 번씩만 풀어 문제를 효율적으로 해결하는 알고리즘 기법이다.
다이나믹 프로그래밍을 구현하는 방법에는
- 작은 문제를 재귀적으로 호출하는 방식인 Top-Down(하향식)
- 작은 문제부터 하나씩 해결해나가면서 답을 도출하는 방식인 Bottom-Up(상향식)
예제 1) 1로 만들기
정수 X가 주어지고 다음 연산을 적절히 사용해서 1을 만드려고 할 때, 연산을 사용하는 횟수의 최솟값을 출력하시오.
- X가 5로 나누어 떨어지면, 5로 나눈다.
- X가 3로 나누어 떨어지면, 3로 나눈다.
- X가 2로 나누어 떨어지면, 2로 나눈다.
- X에서 1을 뺀다.
문제 해설
- Bottom-Up 방식 사용
- 문제의 규칙을 찾아보면 다음과 같다.
f(1) = 0
f(2) = min( f(2-1), f(2/2) ) + 1
f(3) = min( f(3-1), f(3/3) ) +1
f(4) = min( f(4-1), f(4/2) )+ 1
f(5) = min( f(5-1), f(5/5) ) + 1
f(6) = min( f(6-1), f(6/2), f(6/3) ) + 1
.
.
.
- 즉, x를 4개의 연산을 수행하고 그 중에서 가장 작은 값 + 1한 값이 x를 1로 만드는 최소 연산 횟수이다.
- 여기서 1을 더하는 이유는 앞에서 수행한 연산 횟수를 더해주는 것이다.
- 이를 점화식으로 나타내면 다음과 같다.
f(x) = min( f(x-1), f(x/2), f(x/3), f(x/5) ) + 1 (단, x>=2)
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int x = Integer.parseInt(br.readLine());
int[] d = new int[x + 1]; //계산 결과를 저장하기 위한 DP 테이블
for (int i = 2; i <= x; i++) {
d[i] = d[i - 1] + 1; //1을 빼는 경우
if (i % 2 == 0) { //2로 나누어 떨어지는 경우
d[i] = Math.min(d[i], d[i / 2] + 1);
}
if (i % 3 == 0) { //3으로 나누어 떨어지는 경우
d[i] = Math.min(d[i], d[i / 3] + 1);
}
if (i % 5 == 0) { //5로 나누어 떨어지는 경우
d[i] = Math.min(d[i], d[i / 5] + 1);
}
}
System.out.println(d[x]);
}
}
예제 2) 개미 전사
개미 전사는 메뚜기 마을의 일직선으로 된 식량창고에서 식량을 빼앗고자 한다. 이 때, 최소한 한 칸 이상 떨어진 식량창고를 약탈해야 한다. 개미 전사를 위해 식량창고 N개에 대한 정보가 주어졌을 때 얻을 수 있는 식량의 최대값을 구하는 프로그램을 작성하시오.
문제 해설
- Botoom-Up 방식 사용
- i번째 식량창고를 터는 경우와 안 터는 경우의 최대 식량을 비교해서 그중에서 더 큰 값을 구한다.
- i번째 식량창고를 터는 경우: (i-2)번째 식량창고까지의 최대 식량 + i번째 식량창고의 식량
- i번째 식량창고를 안 터는 경우: (i-1)번째 식량창고까지의 최대 식량

- 창고가 1일때부터 차례대로 규칙을 찾아서 식으로 나타내면 다음과 같다.
f(0) = array[0]
f(1) = max( array[0], array[1] )
f(2) = max( f(2-1), f(2-2)+array[2] )
f(3) = max( f(3-1), f(3-2)+array[3] )
.
.
.
- 이를 점화식으로 나타내면 다음과 같다.
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine()); //식량창고의 개수
int[] d = new int[101];
int[] array = new int[n];
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 0; i < n; i++) {
array[i] = Integer.parseInt(st.nextToken());
}
d[0] = 0;
d[1] = Math.max(array[0], array[1]);
for (int i = 2; i < n; i++) {
d[i] = Math.max(d[i - 1], d[i - 2] + array[i]);
}
System.out.println(d[n-1]);
}
}
문제 3) 바닥 공사
가로의 길이가 N, 세로의 길이가 2인 직사각형 형태의 바닥을, 1×2, 2 ×1, 2 ×2의 덮개를 이용해서 채우고자할 때, 바닥을 채우는 몯느 경우의 수를 구하는 프로그램을 작성하시오.
문제 해설
- 문제2)와 같이 N=1일때부터 차례대로 규칙을 찾아보면 다음과 같다.

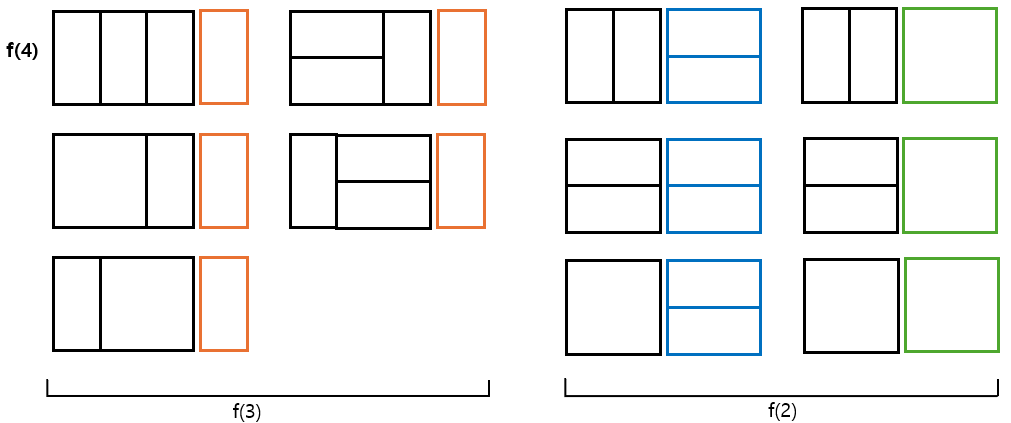
f(1) = 1
f(2) = 3
f(3) = f(2) + f(1) * 2
f(4) = f(3) + f(2) * 2
f(5) = f(4) + f(3) * 2
.
.
.
- 즉, 왼쪽부터 차례대로 바닥을 채운다고 가정하고 다음 두 가지 경우만 고려하면 된다.
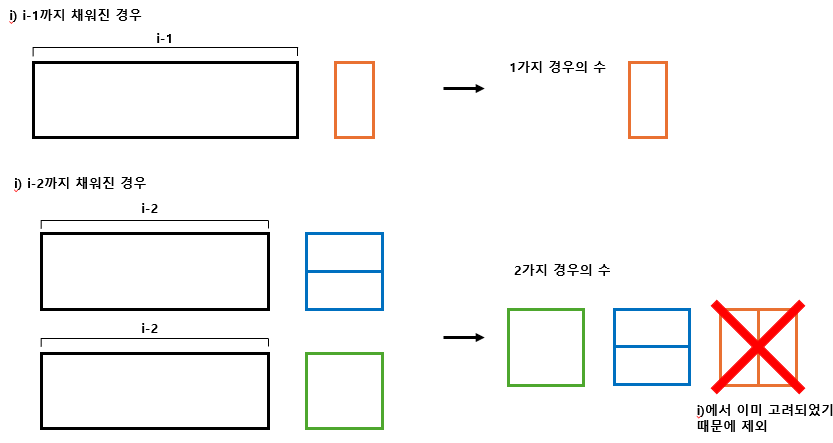
이 규칙으로 점화식을 세워보면 다음과 같다.
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[] dp = new int[n + 1];
dp[1] = 1;
dp[2] = 3;
for (int i = 3; i <= n; i++) {
dp[i] = (dp[i - 1] + dp[i - 2] * 2) % 796796;
}
System.out.println(dp[n]);
}
}
문제 4) 효율적인 화폐구성
N가지 종류의 화폐가 있을 때, 이 화폐들의 개수를 최소한으로 이용해서 그 가치의 합이 M원이 되도록 하려고 한다. 각 화폐는 몇 개라도 사용할 수 있고, 사용한 화폐 구성은 같지만 순서만 다른 것은 같은 것을 구분한다.
문제 해설
- 금액 i와 i를 만들기 위해 마지막으로 사용한 화폐를 k라고 하면,
- 이를 점화식으로 나타내면 아래와 같다.
f(x-k)를 만드는 방법이 존재하는 경우: f(x) = min(f(x), f(x-k) + 1)
f(x-k)를 만드는 방법이 존재하지 않는 경우 : f(x) = 10001
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken()); //화폐 종류의 수
int m = Integer.parseInt(st.nextToken()); //원하는 금액
int[] money = new int[n]; //화폐를 담는 배열
int[] dp = new int[m + 1]; //최소 화폐 개수를 담는 dp 테이블
for (int i = 0; i < n; i++) {
money[i] = Integer.parseInt(br.readLine());
}
//dp 테이블 초기화
dp[0] = 0;
for (int i = 1; i < m + 1; i++) {
dp[i] = 10001;
}
//1원~m원까지 dp 실행
for (int i = 1; i <= m; i++) {
for (int j = 0; j < n; j++) {
if (i - money[j] >= 0) {
dp[i] = Math.min(dp[i], dp[i - money[j]] + 1);
}
}
}
if (dp[m] != 10001) {
System.out.println(dp[m]);
} else {
System.out.println(-1);
}
}
}
[참고]
이것이 취업을 위한 코딩 테스트다 with 파이썬
'PS > 이코테' 카테고리의 다른 글
| [이코테][Java] 편집거리 (0) | 2025.04.27 |
|---|---|
| [이코테][Java] 못생긴 수 (0) | 2025.04.13 |
| [이코테][Java] 정수 삼각형 (0) | 2025.04.12 |
| [이코테][Java] 금광 (0) | 2025.04.10 |
| [이코테][Java] 경쟁적 전염 (0) | 2025.02.14 |